重力の求め方:万有引力と遠心力
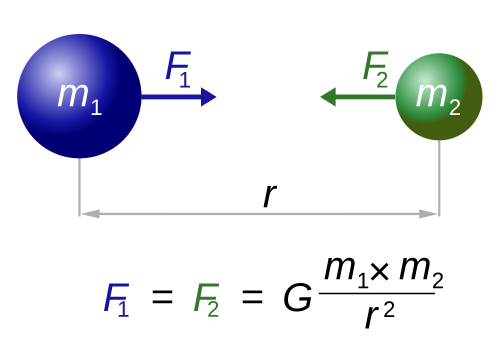
全ての物体には引き合う力が働いており、これを万有引力と呼ぶ。万有引力は以下の式で表される。
F1 = F2 = G × (m1 × m2) / r2
(G:万有引力定数=6.67428×10-11m3/(kg・s2)、m:物体の質量(kg)、r:物体間の距離(m))
式だけではわかりにくいので、図にすると以下のようになる。
地球は自転しているため、遠心力が働いている。遠心力による外向きの力は下の式で表される。
f = mrω2
(m:物体の質量(kg)、r:回転の半径(m)、ω:角度則(rad/s))
重力は万有引力と遠心力の合力である。つまり、重力は単純に地球の中心に向かって働いているわけではない。重力が働く方向を鉛直線と呼ぶ。しかし、殆ど場合、遠心力による力は無視できるほど小さい。
W = mg
(g:重力加速度(m/s2))
gの大きさは場所によって違いはあるが、約9.8m/s2である。
重力と緯度の関係
遠心力は赤道上で最も強く働く。一方、自転の軸である北極・南極では遠心力は働かない。そのため、測定緯度が極に近づくほど重力の値は最も大きくなる。つまり、赤道直下で体重を計ると、極で計った時よりも僅かに軽くなるという現象が起こる。
地球を回転楕円体としたときの、各緯度での計算上の重力を標準重力と呼び、その値は加速度m/s2で表される。赤道と極とでは0.05m/s2の差がある。
重力の測定:重力計
重力を測定する際には、おもりをつけたバネの伸びを観測する方法がある。そのような装置を重力計と呼ぶ。他にも、真空中で物体を落下させて時間を計る方法もある。

重力の補正
重力は物体から離れれば小さくなるため、地表からの高度が高くなるほど重力の値も小さくなる。そのため、その地点の重力の大きさを知るためには様々な補正をしなければならない。補正にはフリーエア補正、地形補正、ブーゲー補正などがある。
ジオイドとは
その土地の平均的な海面の高さをジオイドと呼ぶ。ジオイドとはある意味仮想的な平均海水面で、陸地にも適応できる考え方である。
たとえば、密度がとても高い物質が湖の底に沈んでいた場合、その物質は高い重力が発生しているため、その周辺の水面は盛り上がるはずである。
そう考えると、水面は一様に平というわけではなく、その土地にある物質の密度等によって差が生じる(むしろでこぼこ)ものであると言える。そのデコボコ(重力の差)を視覚的に理解できるしたのが、ジオイドである。
もし地球内部の密度が均一ならばジオイドは完ぺきな地球楕円体となるはずであるが、実際はそうではなく、複雑な起伏がある。最も低いところではインド洋で最小-100m、最も高いところでは東南アジアで+80mとなる。

