地球から見える惑星の運動
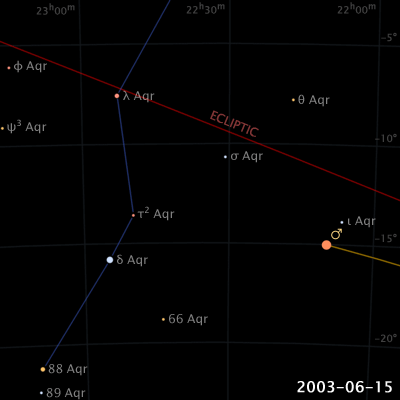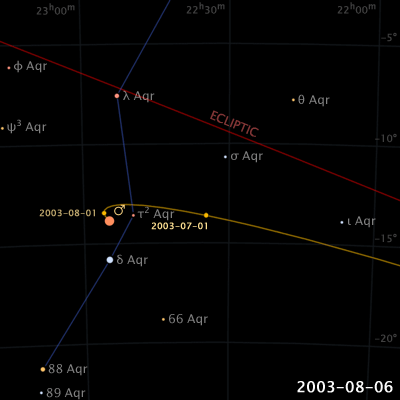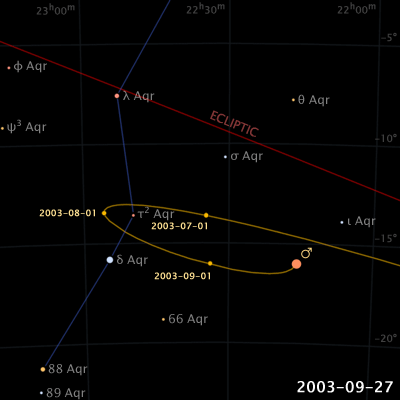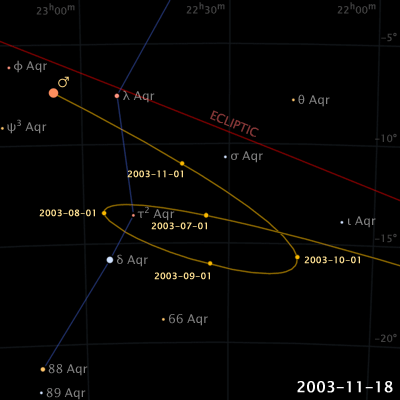
惑星は黄道に沿って西から東へ動いています。これを順行と呼びます。しかし、地球の公転速度が地球の外にある惑星(火星など)よりも早いために、東から西動く「逆行」や、止まって見える「留」などの現象が見られます。
内惑星と外惑星
地球よりも内側の周期に存在する惑星を内惑星(水星、金星)、外側に存在する惑星(火星・木星・土星など)を外惑星と呼びます。それぞれの惑星では、位置によって見え方が異なります。
内惑星の位置と見えやすさ
内惑星の位置によって、名前が付けられており、太陽との兼ね合いで見えやすさが異なっています。
- 外合:地球から見て太陽の裏側に存在する位置。見えにくい。
- 打合:地球と太陽の間に存在する位置。見えにくい。
- 東方最大離角:東側に最大の角度をとることができる位置。日没後に西の空に出現する。
- 西方最大離各:西側に最大の角度をとることができる位置。日の出前に東の空に出現する。
外惑星の位置と見えやすさ
外惑星の位置によって、名前が付けられており、太陽との兼ね合いで見えやすさが異なっています。
- 合:地球から見て太陽の裏側に存在する位置。見えない。
- 衝:地球から見て太陽から正反対の位置。一晩中見える。
- 西矩(せいく):太陽と地球に対して西側に直角に存在する位置。夜半から日の出までにかけて東から南の空に見える。
- 東矩(せいく):太陽と地球に対して東側に直角に存在する位置。日没後から夜半にかけて南から西の空に見える。
内惑星の日面通過
内惑星の場合、太陽面を東から西へ通過するのが見られることがあります。これを日面通過と呼びます。水星や金星が内合の時に見られます。
ケプラーの法則とは?
ケプラーは惑星の運動に関する3つの法則を見出しました。
第一法則(楕円軌道の法則)
惑星の軌道は太陽を焦点の1つとする楕円である。
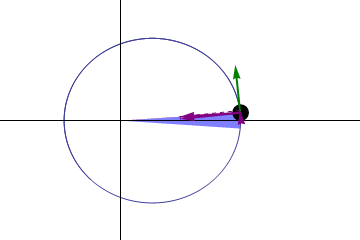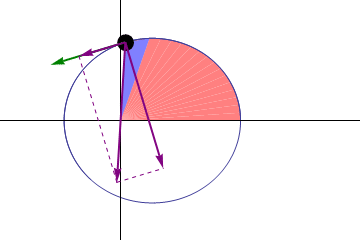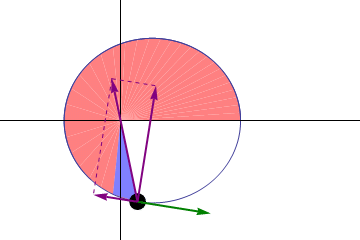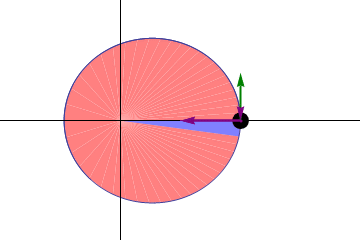
第二法則(面積速度一定の法則)
太陽と惑星を結ぶ線分が、等しい時間におおう面積は等しい(下画像の青色の面積は常に一定である)。
第三法則(調和の法則)
惑星と太陽の間の平均距離の3乗と、惑星の公転周期の2乗との比は、どの惑星をとっても一定である。惑星の平均距離をα、公転周期をPとすると、次の式が成り立つ。
ケプラーの法則が意味するものとは?
第一法則は、惑星の軌道が真円ではなく楕円であることと、太陽の位置は楕円の中心ではなく焦点の1つであることを述べています。
第二法則は、太陽に近いところでは惑星は速度を増し、太陽から遠いところでは惑星は速度を落とすことを意味しています。
第三法則は、公転周期の長さは楕円軌道の長半径のみに依存して決まることを意味しています。
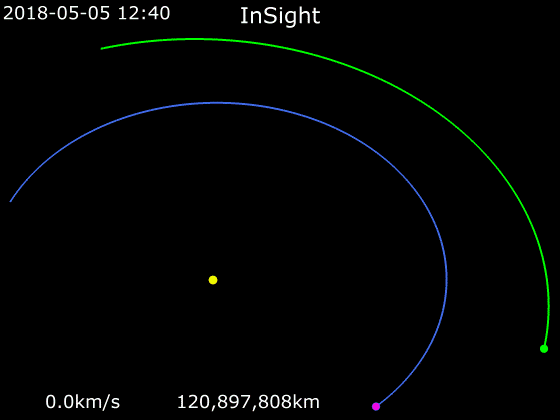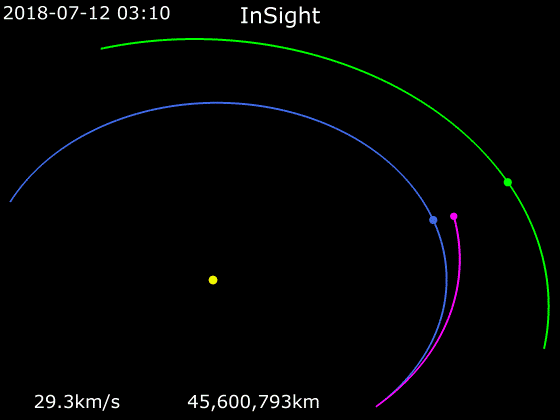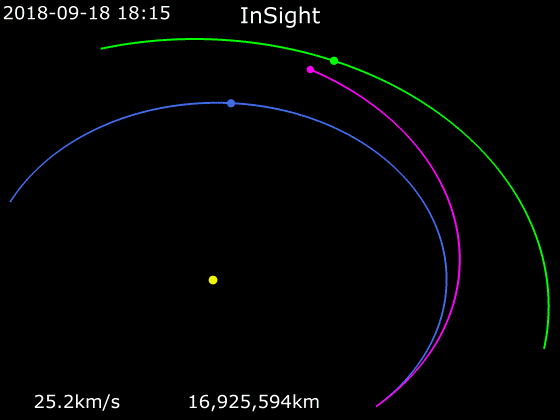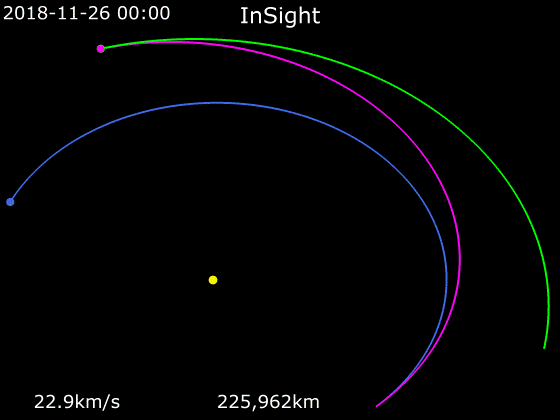
ホーマン軌道とは?
ホーマン軌道は、惑星探査機などが他の惑星の軌道に移る際に考えられた軌道です。内側の惑星の軌道を出発する時と、外側の軌道に達する時に加速して、軌道を移動します。