論理演算と論理回路
コンピュータは1と0の2つの値で計算を行っています。これを論理演算と呼びます。OR、AND、NOTなどが代表的な論理演算です。
論理演算を実際に行う回路を論理回路と呼びます。CPUには論理演算を行う回路が組み込まれています。論理回路はMIL記号で図式化し、真理値表で表現したりします。
基本回路とは
論理和回路(OR回路)、論理積回路(AND回路)、否定回路(NOT回路)の3つを基本回路と呼びます。
論理和回路
入力の一方が1であれば、出力は1になります。
論理積回路
入力の両方が1であれば、出力は1になります。
否定回路
入力が1であれば出力は0、入力が0であれば出力は1になります。
基本回路の組み合わせ
基本回路を組み合わせて作成された回路として、排他的論理和回路(EOR回路)、否定論理和回路(NOR回路)、否定論理積回路(NAND回路)などがあります。
排他的論理和回路
入力が異なれば、出力は1になります。
否定論理和回路
どちらも入力が0のとき、出力が1になります。NOT(A OR B)の意味です。
否定論理積回路
両方の入力がどちらも1以外の時、出力が1になります。NOT(A AND B)の意味です。AND回路の否定と考えておけば良いでしょう。
ビット演算とは
ビット列と特定のビット列を演算させることで、特定のビットを取り出すことができます。この演算させる特定のビット列のことをマスクパターンと呼びます。
ビットの取り出し
例えば次のようなビット列があったとしましょう。
00110001
マスクパターンとして00001111を用意し、論理積(AND)をとります。
00001111
すると下位4ビットのみを取り出すことができました。このようにある特定のビットを取り出すには、1でANDをとれば実行することができます。
ビットの反転
特定のビットを反転させるのには、1でEORをとれば実行することができます。
00001111
EORをとってみると次のようになります。
下位4ビットのみ反転させることができました。
半加算器と全加算器
論理和の組み合わせで加算を行うことができます。2進数の加算を行う回路を加算器と呼びます。
半加算器
半加算器は単純に1桁の2進数の足し算です。真理値表に表すと次のようになります。XとYを加算する数、Sを出力する数の1桁目、Cを出力する数の2桁目とします。
| 入力 | 入力 | 出力 | 出力 |
| X | Y | C | S |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
CはXとYが両方1の時に1となるため、論理積(AND)であることがわかります。SはXとYが異なる値の時のみ1となるため、排他的論理和(XOR)であることがわかります。
論理回路のみで1桁の数の加算を表現することができました。
全加算器
全加算器は、3桁の数を加算する際に使います。例えば、11+11=110ですが、これを論理積で表現するにはどうすれば良いでしょうか。
1桁目は、半加算器を使えば計算できます。2桁目は、1桁目を計算した時に生じる桁上がりを考慮しなければなりません。桁上がりをC’として、真理値表で表現すると次のようになります。
| 入力 | 入力 | 入力(桁上がり) | 出力(3桁目) | 出力(2桁目) |
| X | Y | C’ | C | S |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |
C1桁目を半加算器で計算することによって得ることができます。
wikiからもってきた下図ではXがA、YがB、C’がXとなっていますが、少し説明したいと思います。
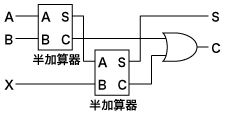
Cの値は、XとYを半加算器によって計算し、さらにその値の1桁目をC’と半加算器で計算して2桁目Cを取得し、初めに得られたCの値とORをとることで得られます。また、ここで得られた1桁目Sはそのまま値として出力します。

